Die Schalldämmungen von Holzständerwänden werden nicht ausschließlich über die Doppelwandresonanz, die Massen der Bauteile und die Koinzidenzgrenzfrequenz bestimmt. Einen nicht unwesentlichen Einfluß üben Eigenmoden (Eigenschwinungen) der Beplankungen aus. Bedingt durch das Ständerraster bauchen die Beplankungen bei bestimmten Frequenzen besonders stark aus. Man kann sich dieses Verhalten in etwa wie das Schwingen einer Gitarrensaite vorstellen.
Auf dieser Seite sind beispielhaft einige Bilder dargestellt, die das Schwingungsverhalten visualisieren. Die Messungen wurden im Rahmen einer Diplomarbeit im Labor für Schall- und Wärmemeßtechnik durchgeführt [1],[2]. Mittels Körperschallaufnehmer wurden auf einer 2,63 x 3,37 m großen Wand die Beschleunigungen von 1540 Messpunkten ermittelt. Die Wand wurde mit Luftschall (weißes Rauschen) angeregt und die Spektren der Messpunkte mittels einer FFT gemessen. Den beiden folgenden Abbildungen kann man die Lage der Ständer und die Verteilung der Messpunkte entnehmen.
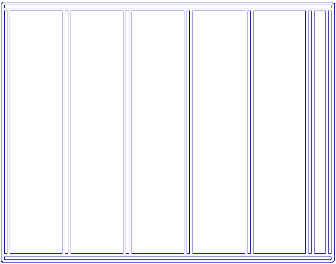
Ständerwerk der Wand

Messpunkte auf der Beplankung
Zur Visualisierung wurden den Beschleunigungspegel Farben zugeordnet: Rot sind hohe Beschleunigungspegel, d.h. große Schwingungsenergien, der Farbe Blau entsprechen geringen Schwingungsenergien. Im folgenden sind in 3 Abschnitten die "schönsten" Schwingungsbilder dargestellt. Durch Anklicken werden die Bilder vergrößert.



























